Matemáticas: Figuras tridimensionales. La pirámide y el cilindro.
La pirámide: Es una figura cuya base es un polígono regular. Cualquiera vale. De los vértices de la base surgen aristas que confluyen en un único vértice, el cénit de la pirámide.
En función de cómo sea la base, así definimos la pirámide. Si su base es un triángulo, pirámide triangular; si es un cuadrado, cuadrangular; si es un pentágono, pentagonal; y así sucesivamente.
El volumen de la pirámide es algo muy bonito. Para entenderlo vamos a ver el desarrollo lógico de la fórmula. Vamos a mirar este dibujo un rato:
Dado un prisma triangular, puede ser partido en tres pirámides exactamente iguales. De lo cual se deduce fácilmente que el volumen de la pirámide será 1/3 del volumen del prisma en el que estaba en un principio integrada. Así, la fórmula queda:
Siendo "Ab" área de la base, y "h" la altura de la pirámide.
El principio es aplicable a cualquier tipo de pirámide. Por ejemplo, una cuadrangular:
El cilindro. El cilindro es más fácil:
No os costará mucho deducir que el volumen de un cilindro va a ser... Sí, eso es: el área de la base por la altura. Por lo tanto se calcula el área del círculo de base y luego a multiplicar por la altura.
El cono. Seguimos tirando de deducción:
Un cono es como una pirámide, solo que tiene una sola cara curvada que se cierra sobre sí misma. "Es como una pirámide..."
Por lo tanto, su volumen es el área de la base multiplicado por su altura y luego dividida por tres.
Me queda por explicar el volumen de la esfera... Pero ese ya para mañana, que tiene tela.
Propuesta de ejercicios:
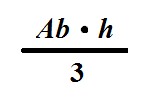
No hay comentarios:
Publicar un comentario