AMAJONIA 6º.: Plan de clases. 13 / 05 / 2021. Volumen de la esfera.

Mates: Vamos a darle tralla al volumen de la esfera, que es complicado de narices. Para ello os contaré una pequeña historieta de Arquímedes.

El cálculo del volumen de la esfera fue uno de los descubrimientos que Arquímedes más estimaba de todos los muchísimos que hizo en su vida. Llegó a demostrar de un modo muy original que el volumen de la esfera es igual a dos tercios del volumen del cilindro circular circunscrito a ella. Tanto le impresionó esto a él mismo que mandó que en su tumba se grabase esta figura en recuerdo de la mejor de sus ideas.

Vamos a ver cómo llegó hasta ahí. Arquímedes se imaginó una semiesfera y junto a ella un cilindro circular recto y un cono recto, ambos de base igual a un círculo máximo de la semiesfera. Algo así.

Arquímedes cortó las tres figuras por un plano paralelo a la base del cilindro y cono (el plano de rayas que corta a las tres figuras) y se preguntó cómo serían las secciones determinadas por este plano en cilindro, semiesfera y cono (en azul). Para que sea más fácil de entender, vamos a dar valores numéricos a estas figuras. Radio y altura van a coincidir en el valor 5. Las secciones están a 2 metros de altura, y por lo tanto a 3 del cénit.

En el cilindro está claro. La sección es igual que la base. Por lo tanto:

Sería 25 x 3,14 = 78,5 unidades cuadradas.

En cuanto a la esfera, hay que afinar un poco más. Tenemos que imaginarnos lo siguiente:

¡Tachaaaan! Aplicando pitágoras, sabemos que r = 4. Ya sólo queda aplicar la fórmula del área del círculo, y nos sale que:

16 x 3,14 = 50,24 unidades cuadradas.

El cono es un poco más complicado. Para calcular el radio de la sección del cono tenemos que tener en cuenta varios aspectos. Miremos el siguiente dibujo:

Sabemos todos estos números menos la "d" que aparece con una interrogación. Sin embargo todo cambia si también sabemos que los ángulos alfa (α) y beta (β) tienen 45º cada uno. Porque siempre que esto pasa en un triángulo... ¡Los catetos son iguales! Como sucede en una escuadra:

Por lo tanto la interrogación de la "d" es igual a 3. Ya solo queda operar:

3,14 x 9 = 28,26 unidades cuadradas.

Luego Arquímedes ordenó los datos:

Área de la sección de la semiesfera: 50,24

Área de la sección del cono: 28,26

Área de la sección del cilindro: 78,50

Guau. Es asombroso. Si sumamos la sección de la semiesfera a la sección del cono, obtenemos la sección del cilindro:

50,24 + 28,26 = 78,50

Esa es la relación entre las tres figuras. Y como es una constante, se puede aplicar al volumen:

Por lo tanto Arquímedes dedujo que el volumen de una semiesfera de radio "r" sumado al volumen de un cono de radio "r" sería igual a un cilindro de radio "r", siempre y cuando los tres tuvieran la misma altura. Maravilloso. Ahora volvamos al ejemplo de antes:

Calculamos el volumen del cilindro: 25 x 3,14 x 5 = 392,5

Calculamos el volumen del cono: (25 x 3,14 x 5) : 3 = 130,83

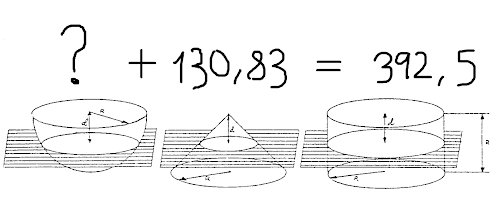
Ya lo que nos queda es súper fácil: